二维数组—求解杨辉三角
课程名称:C语言程序设计
适用专业:计算机应用技术、移动通信技术、信息安全技术应用
案例作者:贾利娟
一、案例的主题
“二维数组—求解杨辉三角”—《C语言程序设计》课程课堂教学中的科学思维、科学伦理、大国工匠精神以及文化自信。
二、结合章节
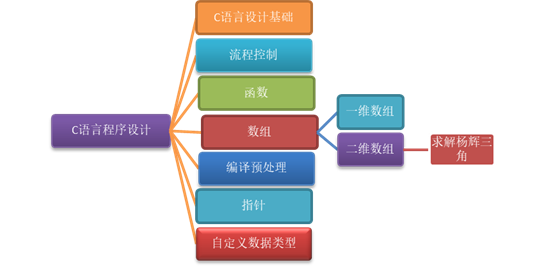
《C语言设计基础》第四部分内容:数组—二维数组,如下图。
教学目标
知识目标
1.掌握二维数组类型变量的定义与引用。
2.掌握数组元素的引用。
3.了解二维数组的基本概念。
能力目标
1.熟练掌握二维数组的基础知识。
2.根据实际需求会用二维数组解决实际问题。
(三)素养目标
1.培养学生自学能力和新知识和新技能的应用能力。
2.培养学生较强的分析问题和解决问题的能力。
3.培养科学思维、积极探索、精益求精、团队合作的工匠精神。
4.培养团队协作意识、责任意识。
5.通过杨辉三角的起源,了解中国古人为世界做出的贡献。
四、案例意义
本课程在开展教学时,使用线上线下混合式教学、“教学做”一体化、案例分析法进行。依据“以学生为中心”的教学理念,以任务驱动法为主,多媒体演示、讲练结合和分组讨论等教学方法辅助教学,优化教学效果。
本节教学内容秉承以学生为主体,教师为主导的教学理念,将培养学生的知识目标、能力目标、素质目标有机结合,最大限度的发挥学生的主观能动性,理论与实践相结合,让学生在轻松愉快的氛围下学习。围绕教学目标,采用课前、课中、课后的教学方式,将多媒体技术和传统的教学手段相结合,利用小组合作学习、案例分析法等,让学生主动学习。通过对杨辉三角起源认知(杨辉是中国宋代著名的数学家,他整理杨辉三角领先于法国数学家帕斯卡近400年,著有《详解九章算法》),激发学生的爱国热情和民族自豪感,同时也让学生树立坚定的信念,向科学家学习,成长为思想政治可靠、专业技术优秀的建设人才。通过杨辉三角的样式,分析模型特点,确定二维数组结构,再到发现递推规律,确定推演公式,最后生成代码等一系列环节,培养学生的建模意识,启发学生的推演思维。
五、教学实施过程
教学实施 |
教学内容 |
教学活动 |
辅助资源 |
教师主导 |
学生主体 |
课前-学新知 |
二维数组的定义、初始化 |
1.发布学习任务 (1)将本次学习内容课件及微课视频上传至云班课。 (2)要求学生完成课前小测试。 (3)要求学生分组完成讨论。 2.关注课前学习:查看学生的资源阅读及下载量。督促没有观看的学生。 |
1.完成学习任务 (1)查阅查阅南宋数学家杨辉、法国数学家帕斯卡的相关资料。 (2)认识、观察并分析杨辉三角的规律。 (3)学习二维数组的定义、初始化。 2.分组完成讨论并整理 |
教学课件 
在线教学资源 
|
设计意图 |
1.利用翻转课堂拓展学生的学习时间及空间,培养学生自主探究、分组 合作学习的能力和意识。 2.通过云班课完成课前学习及测试,了解学生自学情况,梳理学习疑惑和困难以便课上答疑突破。 |
思政元素 |
查阅南宋数学家杨辉、法国数学家帕斯卡的相关资料,了解中国古人为世界做出的巨大贡献,实现文化自信。 |
课中——解疑惑(20分钟) |
二维数组定义及初始化 |
1.课前学习点评。 2.小组展示、调试。 3.教师指导、总结。 验证过程教师巡回指导,指导学生学会通过报错信息调试程序。 4.讲解共性问题 |
1.了解个人课前学习所获经验值(得分情况)。 2.各小组展示程序完成情况并做简单说明。 3.程序出错或未完成的修改课前仿例程序并进行结果验证。 l 余力学生:用两种不同方式完成二维数组的初始化; l 中等学生:完成一种二维数组的初始化; l 后进学生:完成基本数据类型的定义。 4.听看共性问题讲解,查漏补缺。 |
课堂练习案例1截图 


|
设计意图 |
1.通过点评课前学习情况,鼓励学生后续更积极认真的对待课前学习。 2.分层教学,尽量照顾所有层次学生,并通过巡回指导发现学困生,指导理解数组的概念。 |
思政元素 |
1.培养学生的科学思维。 2.通过对课前学习效果的分析及纠错,训练学生细致观察,积极探究,精准编程的能力和习惯,培养敬业、精益和专注的工匠精神。 |
课中——提能力(50分钟) |
二维数组的应用 (求解杨辉三角) |
1.分组探究杨辉三角的样子。 2.分析模型特点,确定二维数组结构。 3.发现递推规律,确定推演公式。 4.教师指导、总结。 5.讲解共性问题。 |
1.学生在教师的点拨下分析杨辉三角的样子,确定二维数组结构。总结杨辉三角的递推规律,确定推演公式。 2.学生小组讨论程序设计思路。 3.学生独立编写程序。 l 余力学生:独立完成杨辉三角程序的编写、调试、运行。 l 中等及后进学生:在老师的指导下完成程序的编写,并能自己通过调试运行出杨辉三角。 |
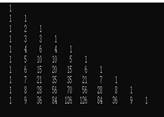

|
设计意图 |
1.通过求解杨辉三角的任务,进一步强化学生对二维数组的理解和运用。 2.培养学生的建模意识,启发学生的推演思维。 |
思政元素 |
1.强烈的爱国情怀,奋发学习刻苦钻研,不畏困难。 2.具有勇于创新的工匠精神,成为有责任感、有创新能力,会学习,有职业理想和家国使命感的人。 |
课中——再登高(20分钟) |
二维数组的应用(矩阵转置) |
1.分组进行案例实现。 将一个二维数组行和列元素互换,存到另一个二维数组中。 2.案例讲解。 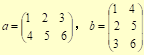
通过写出对应矩阵找出其中的规律 3.总结及作业。 引导学生一起总结本次课所学内容,布置课下任务。 |
1.小组讨论案例实现思路,创建二维数组,编写程序。 2.听老师对同学们共性问题的讲解和演示,查漏补缺。 3.和教师一起总结本次课所学内容。 4.记录课下任务。 |
课堂练习案例3 程序截图 
|
设计意图 |
1.通过分组实现强化团队意识和责任意识。 2.通过故事引入案例,使学生意识到积少成多,坚持不懈的重要性,从而提升学习主动性。 |
思政元素 |
1.培养学生的科学思维。 2.培养勇于探索、试错验证的工匠精神。 |
课后——拓能力 |
大赛题目 提升练习 |
发布作业任务:通过超星学习通发布小组资料查阅任务,并发布、批阅作业,发现问题逐一交流。 |
查看老师发布的资料,自己也可通过网络查阅资料,完成作业任务,提升能力。 |
1、蓝桥杯大赛网站: https://lx.lanqiao.cn/ 2、超星学习通: 二维数组作业 |
设计意图 |
学生通过查阅资料拓展知识面并编程实现,提升学习主动性和解决问题的能力。 |
思政元素 |
1.具有创新意识、严谨求实、吃苦耐劳、科学思维的职业道德。 |
|
|
|
|
|
|
|
|
|
|
六、教学效果评价
本次课按课前(15%)、课中(60%)和课后(25%)三个阶段,依据学习内容及活动形式采用学生自评、教师点评、学生互评、平台打分相结合的方式对学生形成过程性考核评价。
组别 |
|
姓名 |
|
评价 |
阶段 |
标准 |
思政元素 |
分值 |
得分 |
超星平台 (20分) |
课前 |
自学课前资源,完成课前练习作业。 |
学习态度纪律 |
8 |
|
课中 |
上课考勤 |
学习态度纪律 |
2 |
|
课后 |
完成平台作业 |
学习态度纪律 |
10 |
|
学生自评 (15分) |
全过程 |
积极思考,主动探究,精益求精 |
工匠精神、科学思维 |
5 |
|
课中 |
能跟上课堂节奏,注意力集中,能完成相关学习活动。 |
学习态度能力 |
10 |
|
学生互评 (25分) |
全过程 |
能积极参加小组活动 |
团队合作 |
2 |
|
全过程 |
沟通好,能与团队成员合作 |
团队合作 |
2 |
|
全过程 |
能按时完成自己负责的工作 |
责任态度 |
2 |
|
课中 |
独立编写杨辉三角的程序 |
工匠精神 文化自信 |
10 |
|
课中 |
能实现矩阵的转置 |
工匠精神 |
7 |
|
课中 |
不畏困难、严谨求实,勇于创新 |
工匠精神 |
2 |
|
教师评价 (40分) |
课前 |
课前作业正确率 |
学习能力 |
10 |
|
课中 |
专注力高、探究精神、思维活跃 |
学习态度 |
5 |
|
全过程 |
程序实现杨辉三角、矩阵转置 |
学习能力 工匠精神 |
20 |
|
课后 |
完成平台作业 |
学习态度 |
5 |
|
合计 |
100 |
|
七、案例反思
1.学生基本上都理解二维数组的概念,能够实现二维数组初始化的相关代码,能够编程实现较简单的实际问题。但有小部分学生熟练度一般,在编程的过程中花费的时间比较长。
2.在教学过程中,提出有一定难度的问题,使学生感到熟悉又不能单纯地用已有的知识和习惯的方法去解决。使学生进入“心求通而未通,口欲言而不能”的境界,学生自然而然地主动探究寻找答案。
3.引导学生勤于实践。抓好课后练习落实与讲评,常检查,勤督促,对学生存在的问题要及时反馈和讲解,尽量做到教学上少留遗憾。